
Figlia mia,
Tra qualche tempo farai le tue prime esperienze sociali e noterai che, in ogni gruppo, ci saranno delle persone che potrai definire rompiscatole. Sono quelle persone che non si rendono conto di dar fastidio agli altri, o non se ne curano; quelli che buttano le cartacce in giro, non raccolgono i bisogni del cane e lo lasciano abbaiare per tutta la notte; quelli che non rispettano i limiti di velocità vicino alle scuole e parcheggiano sulle strisce pedonali.
Sembrano ovunque! Non puoi né scappare né nasconderti: ti troveranno e ti faranno arrabbiare. Ma forse possiamo capire meglio questo fenomeno e cambiare prospettiva, almeno proviamoci.
Distribuzioni statistiche
La statistica è molto utile per comprendere fenomeni complessi, tra cui i fenomeni naturali e sociali. Ci permette di capire come si distribuiscono i dati, come ad esempio l’altezza delle donne italiane, e quindi rispondere a domande quali: qual è l’altezza media? Quanto è probabile che una persona presa a caso abbia una altezza prossima a quella media? Quanto è probabile che sia alta due metri?
La distribuzione statistica più famosa è quella Gaussiana, non accaso detta anche normale, che ha forma a campana e gran parte dei dati si collocano nei pressi della media. È talmente nota e famosa che spesso assumiamo sia la distribuzione di tutti i fenomeni che osserviamo, ma attenzione, ciò non è vero: non tutti i fenomeni statistici sono gaussiani!
Prendiamo ad esempio due misure: il peso degli uomini di 30 anni ed il loro patrimonio, ossia la loro ricchezza.
Il peso ha una distribuzione gaussiana: in media il peso sarà sui 75kg e gran parte delle persone avranno un peso attorno a quel valore. Certo, ci sarà qualcuno che pesa 40kg ed una manciata di persone ben oltre i 200kg, ma nessuno peserà 750kg, ossia 10 volte la media.
Ora guardiamo alla ricchezza. Il patrimonio medio mondiale è di circa 80.000$ a persona, ma come si distribuiscono le persone rispetto a quel valore medio? Gran parte di esse ha capitali ben inferiori, mentre pochi ultra-ricchi hanno capitali molto più grandi. Ad esempio, Elon Musk ha un patrimonio di 184 miliardi di dollari, 2.3 milioni di volte la media. Ogni Elon Musk contro-bilancia 2.3 milioni di nullatenenti!
La ricchezza non segue una distribuzione normale, ma una distribuzione di Pareto, detta anche “legge di potenza”. La forma delle due curve è molto diversa tra loro, te le disegno:
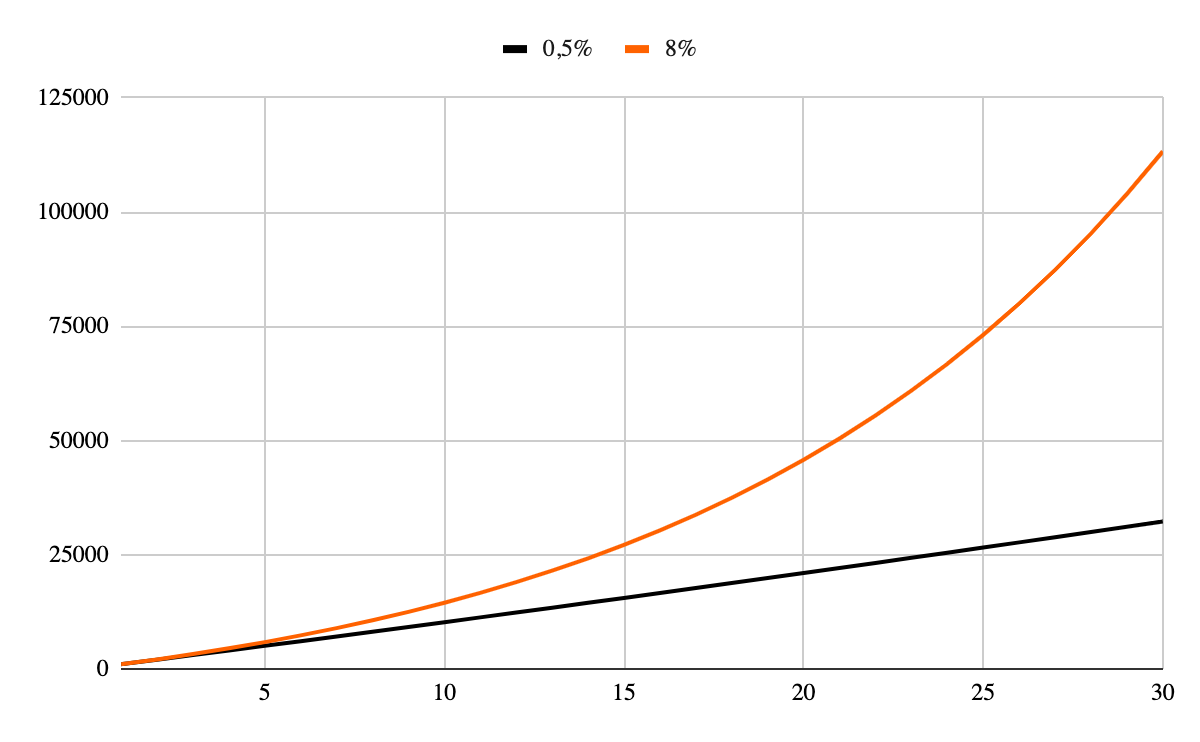
Torniamo ai rompiscatole
Giusto. Cosa c’entra la statistica con i rompiscatole?
Nella nostra scarsa conoscenza della statistica finiamo col pensare che i piantagrane siano ovunque, o anche che tutti noi siamo piantagrane in una certa misura, chi poco più e chi poco meno ma quasi tutti vicini alla stessa quantità media. Entrambe le conclusioni sono sbagliate.
Ad esempio, nel nostro quartiere vivono circa 70 famiglie. Quelle che fanno casino, hanno il cane che abbaia di notte, tengono la musica alta, litigano, parcheggiano l’auto a caso, guidano in modo pericoloso e sporcano le scale coi sacchetti dell’umido che gocciolano sono solo 5 famiglie. Gli altri non contribuiscono in modo apprezzabile al disagio in nessuna delle suddette aree; sono tutte persone per bene, tranquille, collaborative e socievoli.
Si tratta di una chiara distribuzione di Pareto, dove il 10% della popolazione è causa del 90% del disagio. Bene, so cosa ti stai chiedendo: perché è importante capire questo? Non puoi lasciarmi andare a giocare con le mie bambole e smettere di predicare? No.
Capire questo fenomeno è importante perché ti permette di vedere la realtà con più chiarezza e questo è sempre un bene. In questo caso potrai guardare ai tuoi compagni con più empatia e compassione, sapendo che gran parte di loro è solo vittima dei pochi scalmanati. Ti permette anche di isolare chi è problematico e non perdere la fiducia nell’intero genere umano.
Ma c’è anche un ultimo aspetto che ti può interessare.
La distribuzione degli eroi
Così come i rompiscatole, gli eroi del quartiere sono una manciata. C’è un signore che pulisce dove gli altri sporcano, senza chiedere nulla in cambio; una signora riprende chi lascia i bisogni del cane in giro, rischiando insulti e ritorsioni; un altro saluta sempre tutti col sorriso e gli augura buona giornata, anche chi non ha mai visto prima.
Quanti sono? Pochissimi, ma il loro impatto positivo sul quartiere è sproporzionato: si tratta ancora una volta di una distribuzione di Pareto.
Ed ecco qui la morale di questa mia lettera: tu, figlia mia, puoi fare la differenza. Gran parte delle persone fa da spettatore alla vita, tu “sii il cambiamento che vuoi vedere nel mondo” (Gandhi). Ti sembrerà difficile, ma lo è meno di quello che sembra: non dovrai contrastare gran parte delle persone, solo pochissimi. E gli altri faranno il tifo per te, io per primo.
Copertina by <a href="https://unsplash.com/@rhindaxu?utm_source=unsplash&utm_medium=referral&utm_content=creditCopyText">Linda Xu</a> on <a href="https://unsplash.com/?utm_source=unsplash&utm_medium=referral&utm_content=creditCopyText">Unsplash</a>
Sosteniamoci
- Prima Assicurazioni: per RCA, casa e compagnia.
- Vite Sicure: assicurazione TCM 🤘
- American Express Payback: regala soldi a chi si iscrive.
- BBVA. Buon conto. Per 10€ regalo usa: 77660079210471
- Conto Credit Agricole. Buoni Amazon cicciosi!

